Exploring data I
Lecture 4
Duke University
STA 199 - Fall 2024
September 10, 2024
Warm-up
While you wait…
Prepare for today’s application exercise: ae-04-gerrymander-explore-I
Go to your
aeproject in RStudio.Make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
Click Pull to get today’s application exercise file: ae-04-gerrymander-explore-I.qmd.
Wait till the you’re prompted to work on the application exercise during class before editing the file.
Announcements
Weekend office hours in Old Chem – bring your Duke Card, you’ll need to swipe/tap in to get in
AEs are due by the end of class (precisely, by 2 pm) – done = at least one commit + push
Coding principles bonus office hour, RSVP at https://forms.gle/mufcsHnPXejZbkdT8 – Thursday, 9/12 at 7:30 pm at Old Chem 116
-
RStudio visual editor acting up?
Using Chrome – make sure to update!
Using another browser or update doesn’t solve the problem, come by my office hours to diagnose
New resource: Code along videos
Any questions about lab before we get started?
Exploratory data analysis
Packages
- For the data: usdata
── Attaching core tidyverse packages ────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.3 ✔ tidyr 1.3.1
✔ purrr 1.0.2
── Conflicts ──────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsData: gerrymander
# A tibble: 435 × 12
district last_name first_name party16 clinton16 trump16 dem16 state
<chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <chr>
1 AK-AL Young Don R 37.6 52.8 0 AK
2 AL-01 Byrne Bradley R 34.1 63.5 0 AL
3 AL-02 Roby Martha R 33 64.9 0 AL
4 AL-03 Rogers Mike D. R 32.3 65.3 0 AL
5 AL-04 Aderholt Rob R 17.4 80.4 0 AL
6 AL-05 Brooks Mo R 31.3 64.7 0 AL
7 AL-06 Palmer Gary R 26.1 70.8 0 AL
8 AL-07 Sewell Terri D 69.8 28.6 1 AL
9 AR-01 Crawford Rick R 30.2 65 0 AR
10 AR-02 Hill French R 41.7 52.4 0 AR
# ℹ 425 more rows
# ℹ 4 more variables: party18 <chr>, dem18 <dbl>, flip18 <dbl>,
# gerry <fct>What is gerrymandering?
Data: gerrymander
What is a good first function to use to get to know a dataset?
Data: gerrymander
Rows: Congressional districts
-
Columns:
Congressional district and state
2016 election: winning party, % for Clinton, % for Trump, whether a Democrat won the House election, name of election winner
2018 election: winning party, whether a Democrat won the 2018 House election
Whether a Democrat flipped the seat in the 2018 election
Prevalence of gerrymandering: low, mid, and high
Variable types
| Variable | Type |
|---|---|
district |
categorical, ID |
last_name |
categorical, ID |
first_name |
categorical, ID |
party16 |
categorical |
clinton16 |
numerical, continuous |
trump16 |
numerical, continuous |
dem16 |
categorical |
state |
categorical |
party18 |
categorical |
dem18 |
categorical |
flip18 |
categorical |
gerry |
categorical, ordinal |
Univariate analysis
Univariate analysis
Analyzing a single variable:
Numerical: histogram, box plot, density plot, etc.
Categorical: bar plot, pie chart, etc.
Histogram - Step 1

Histogram - Step 2
Histogram - Step 3
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.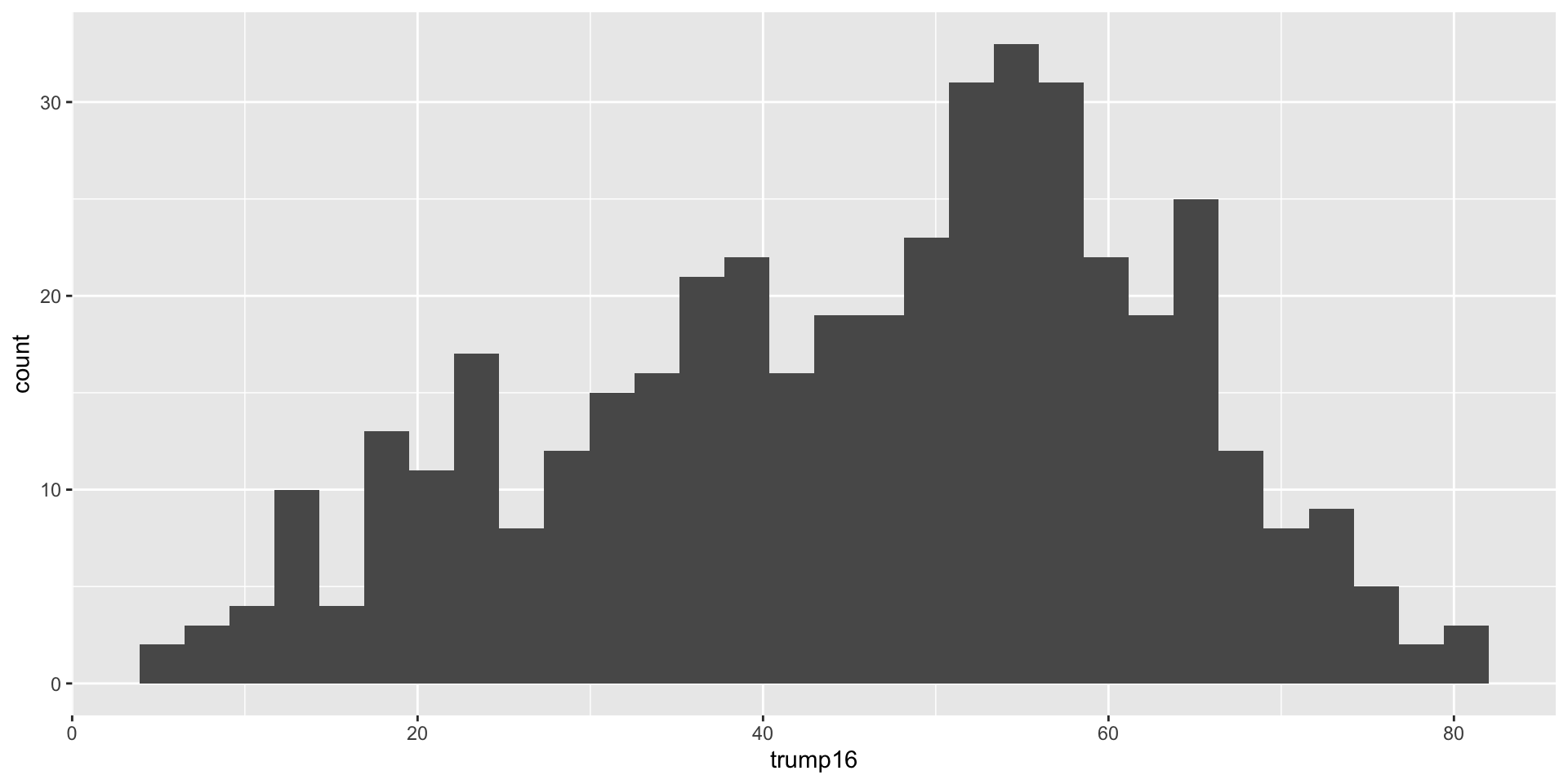
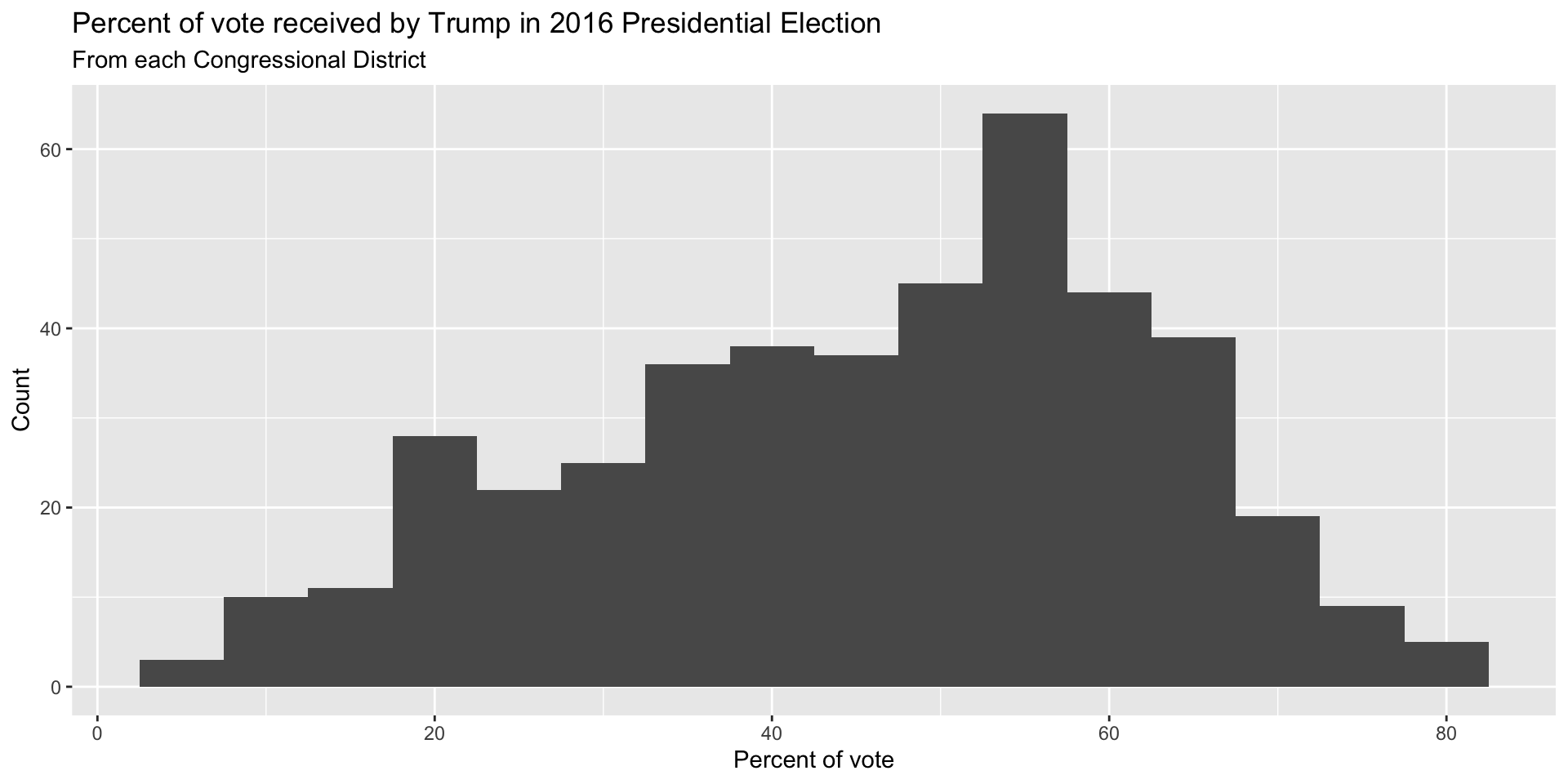
Histogram - Step 4
Histogram - Step 5
Box plot - Step 1

Box plot - Step 2
Box plot - Step 3
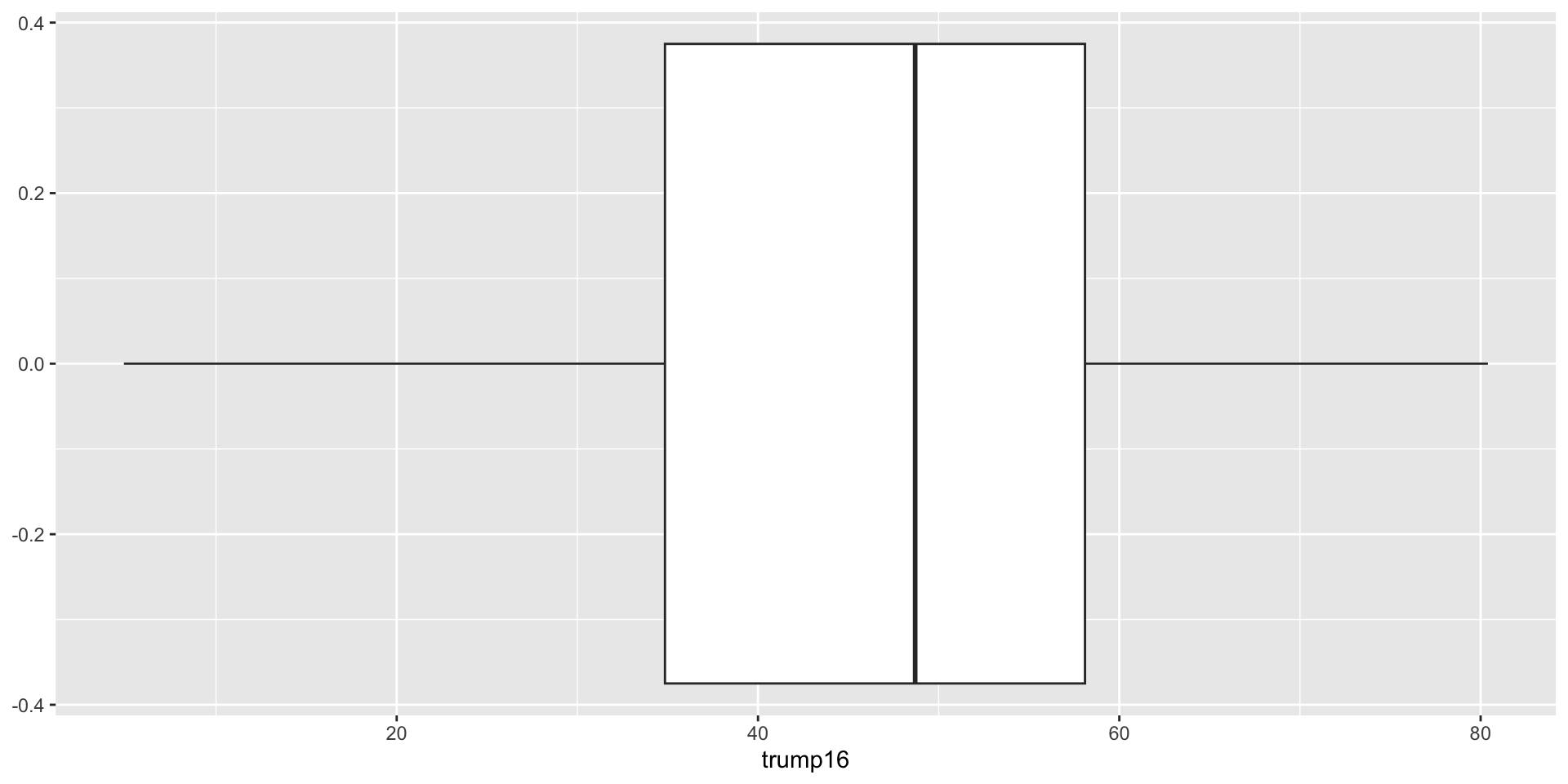
Box plot - Alternative Step 2 + 3
Box plot - Step 4
Density plot - Step 1

Density plot - Step 2
Density plot - Step 3
Density plot - Step 4
Density plot - Step 5
Density plot - Step 6
Density plot - Step 7
Density plot - Step 8
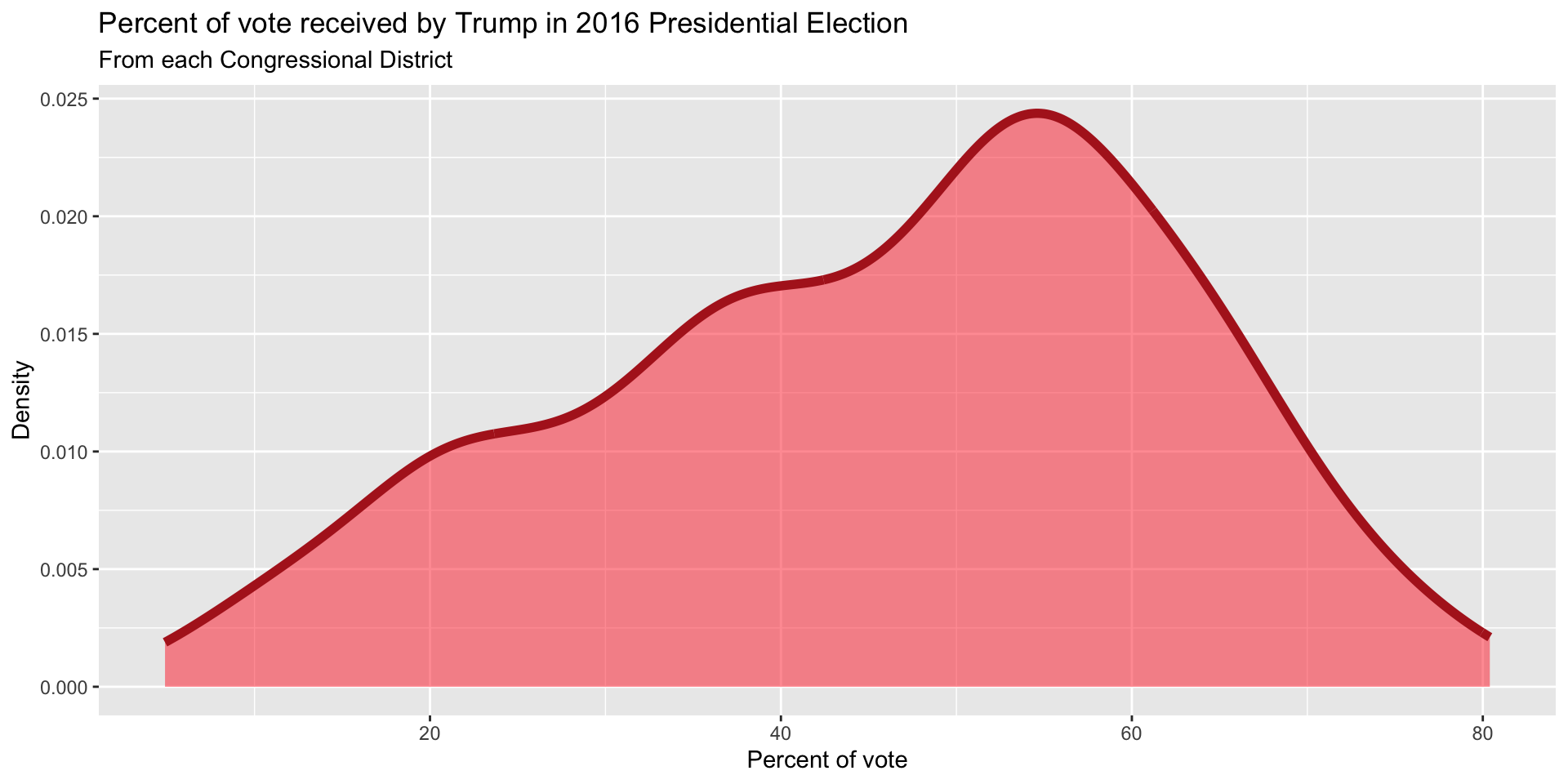
Summary statistics
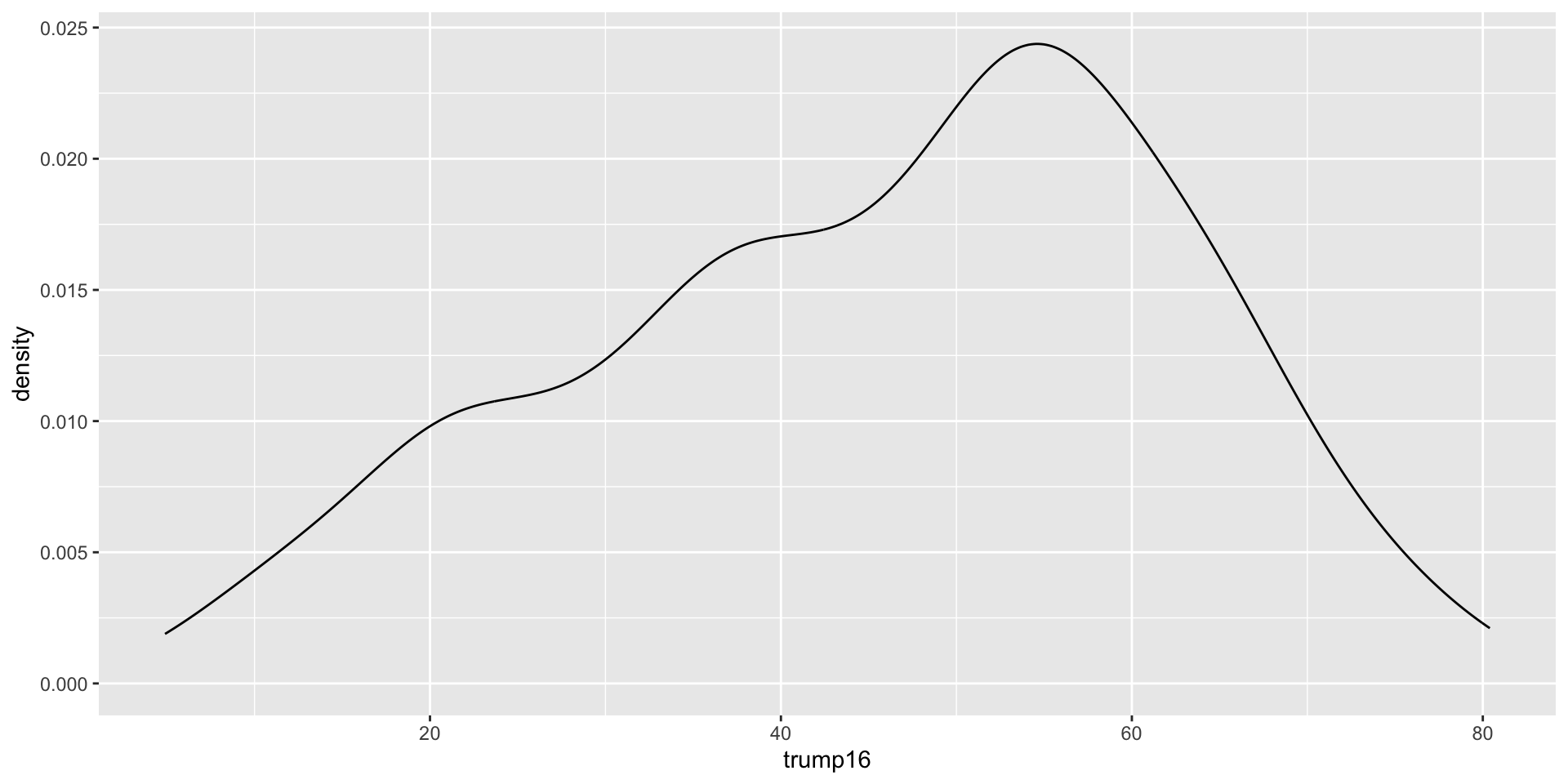
Distribution of votes for Trump in the 2016 election
Describe the distribution of percent of vote received by Trump in 2016 Presidential Election from Congressional Districts.
Shape: The distribution of votes for Trump in the 2016 election from Congressional Districts is unimodal and left-skewed.
Center: The percent of vote received by Trump in the 2016 Presidential Election from a typical Congressional Districts is 48.7%.
Spread: In the middle 50% of Congressional Districts, 34.8% to 58.1% of voters voted for Trump in the 2016 Presidential Election.
Unusual observations: -
Bivariate analysis
Bivariate analysis
Analyzing the relationship between two variables:
Numerical + numerical: scatterplot
Numerical + categorical: side-by-side box plots, violin plots, etc.
Categorical + categorical: stacked bar plots
Using an aesthetic (e.g., fill, color, shape, etc.) or facets to represent the second variable in any plot
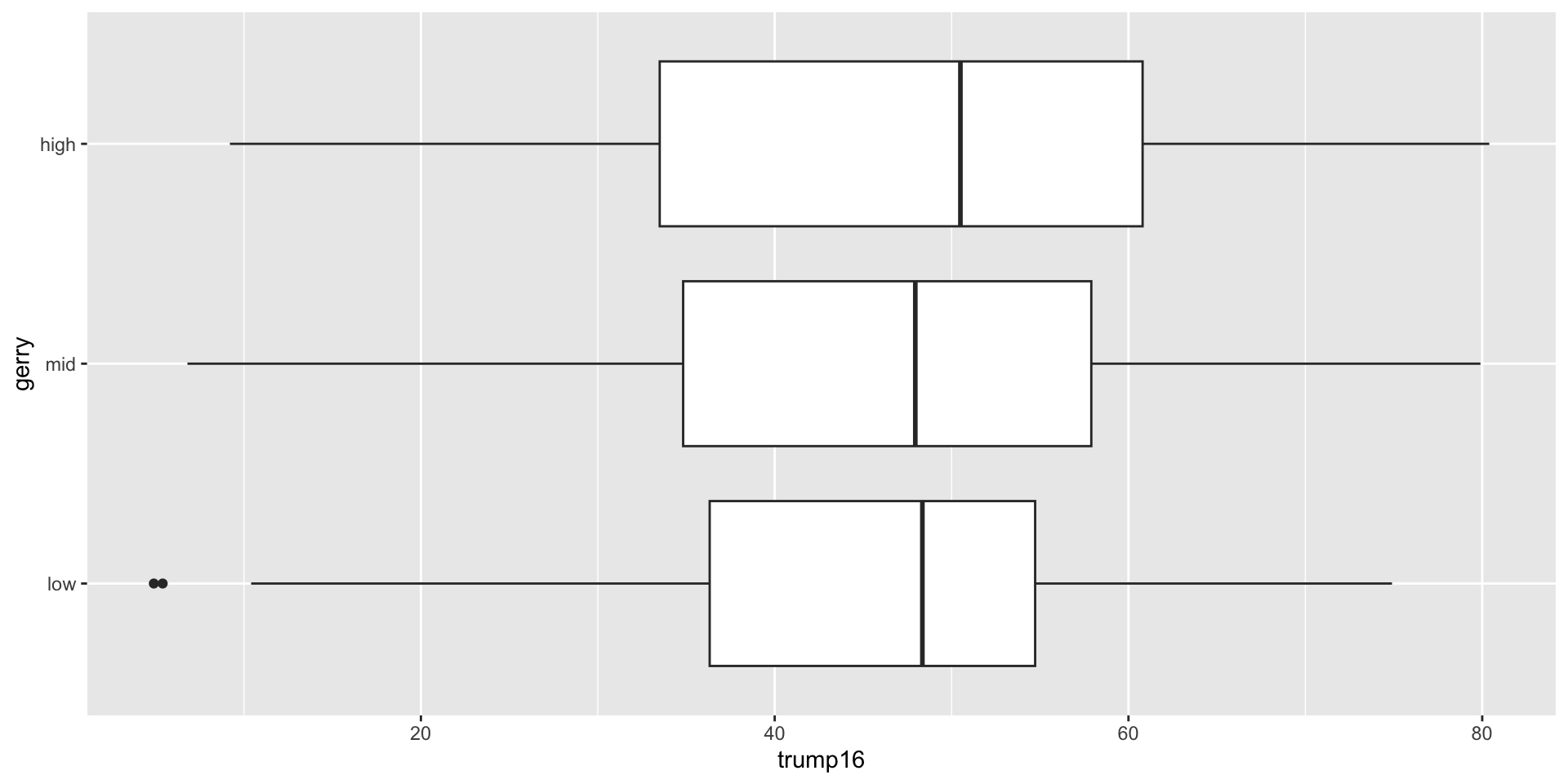
Side-by-side box plots
Summary statistics
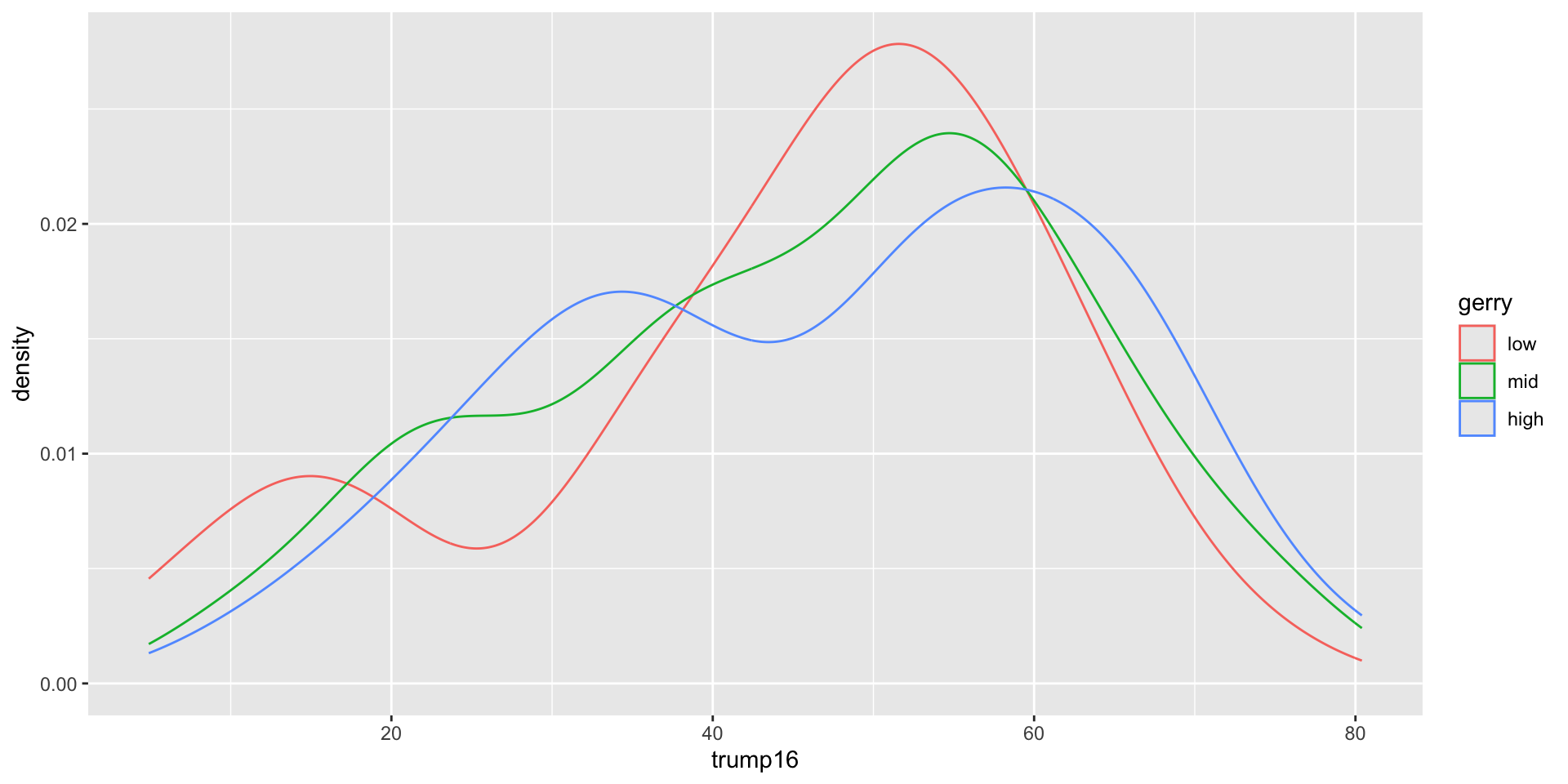
Density plots
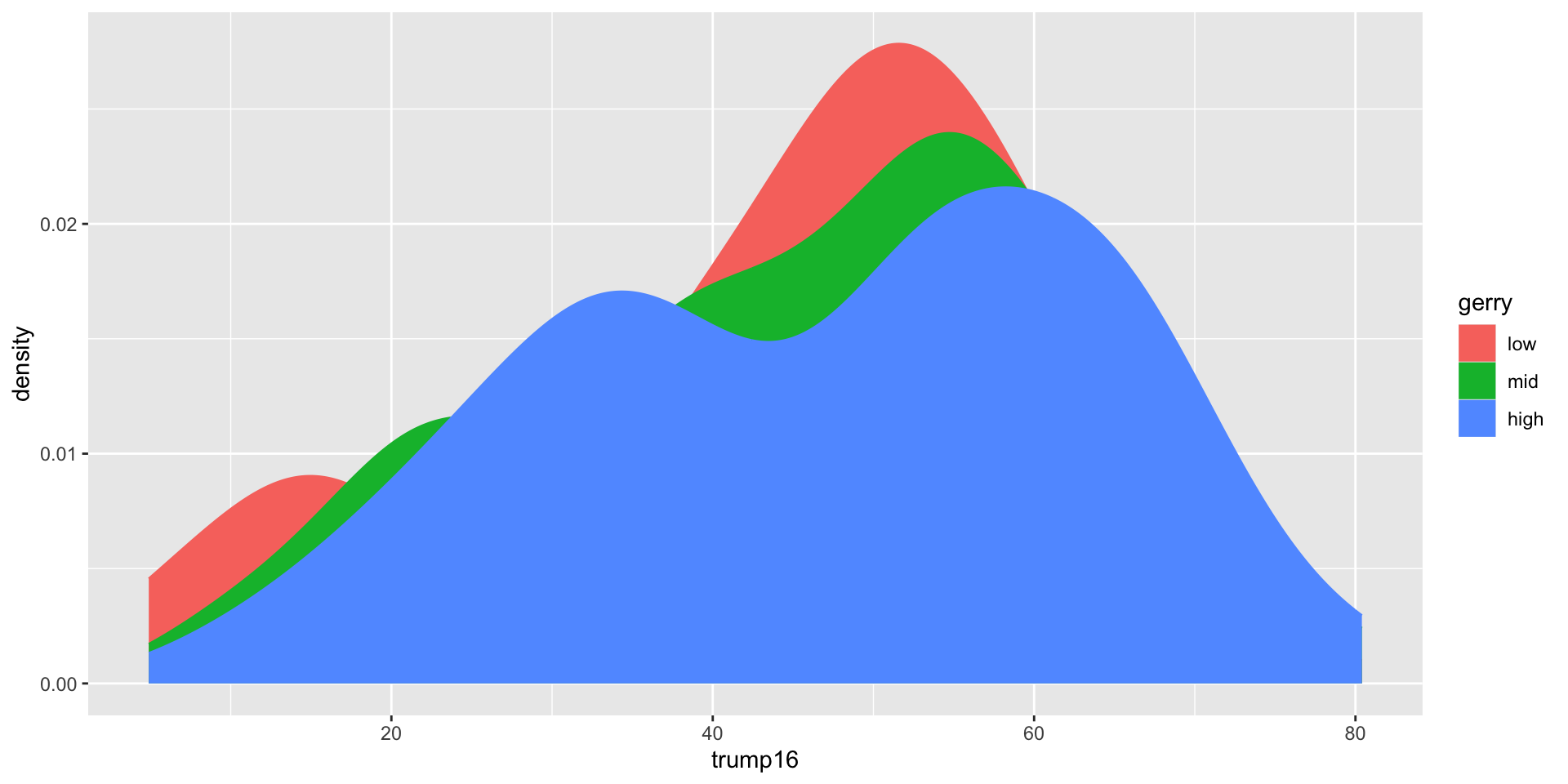
Filled density plots
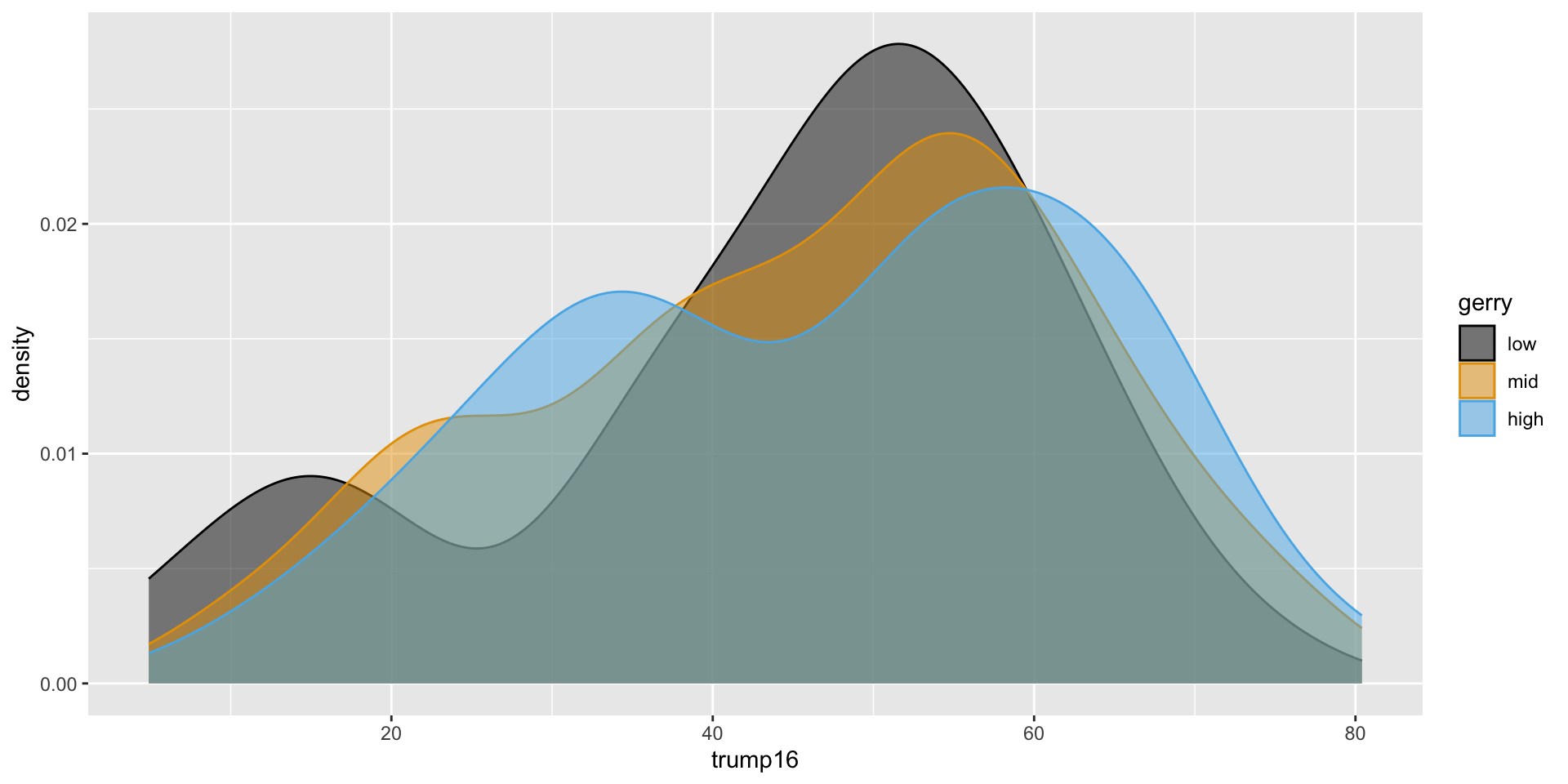
Better filled density plots
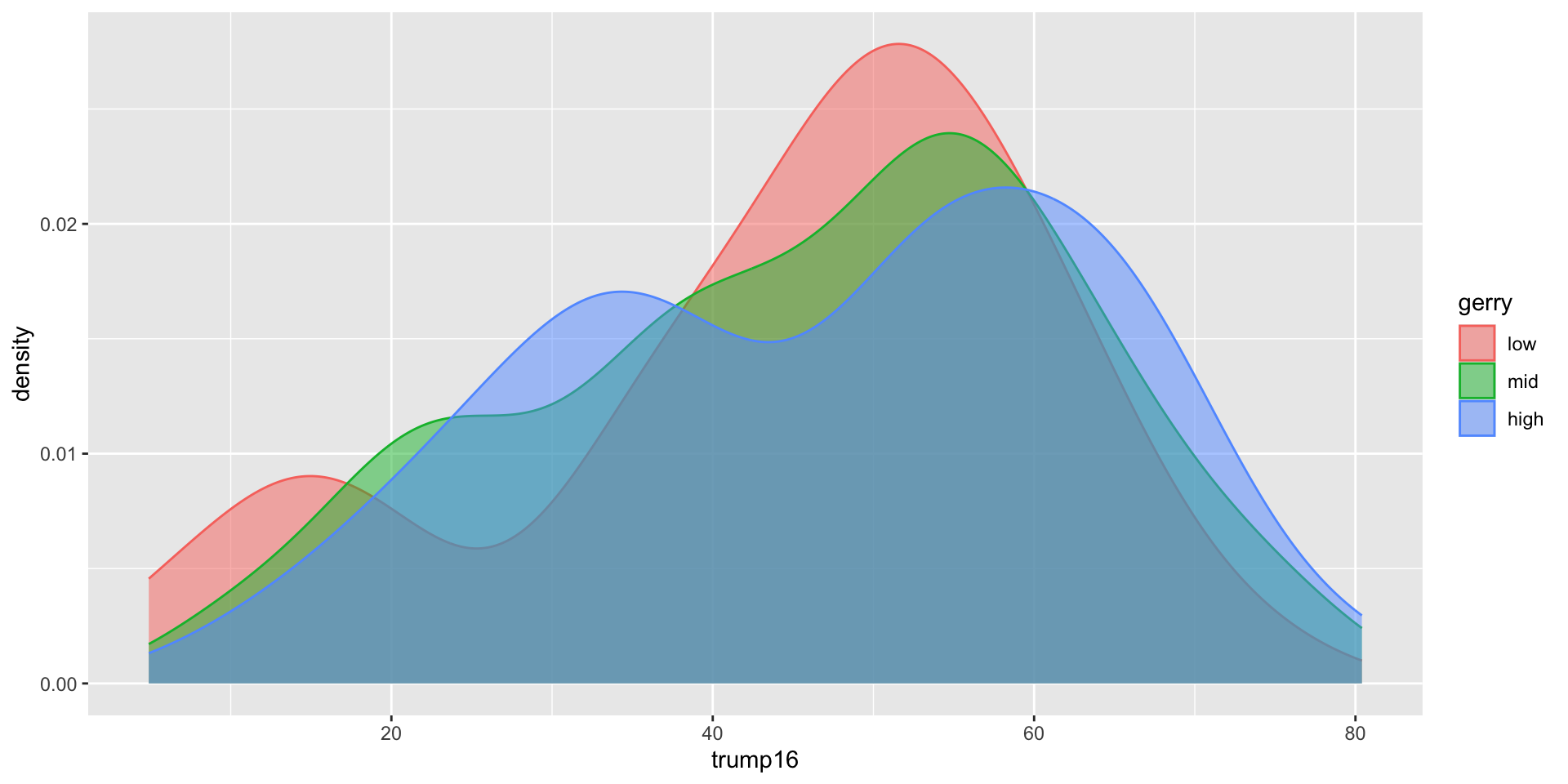
Better colors
Violin plots
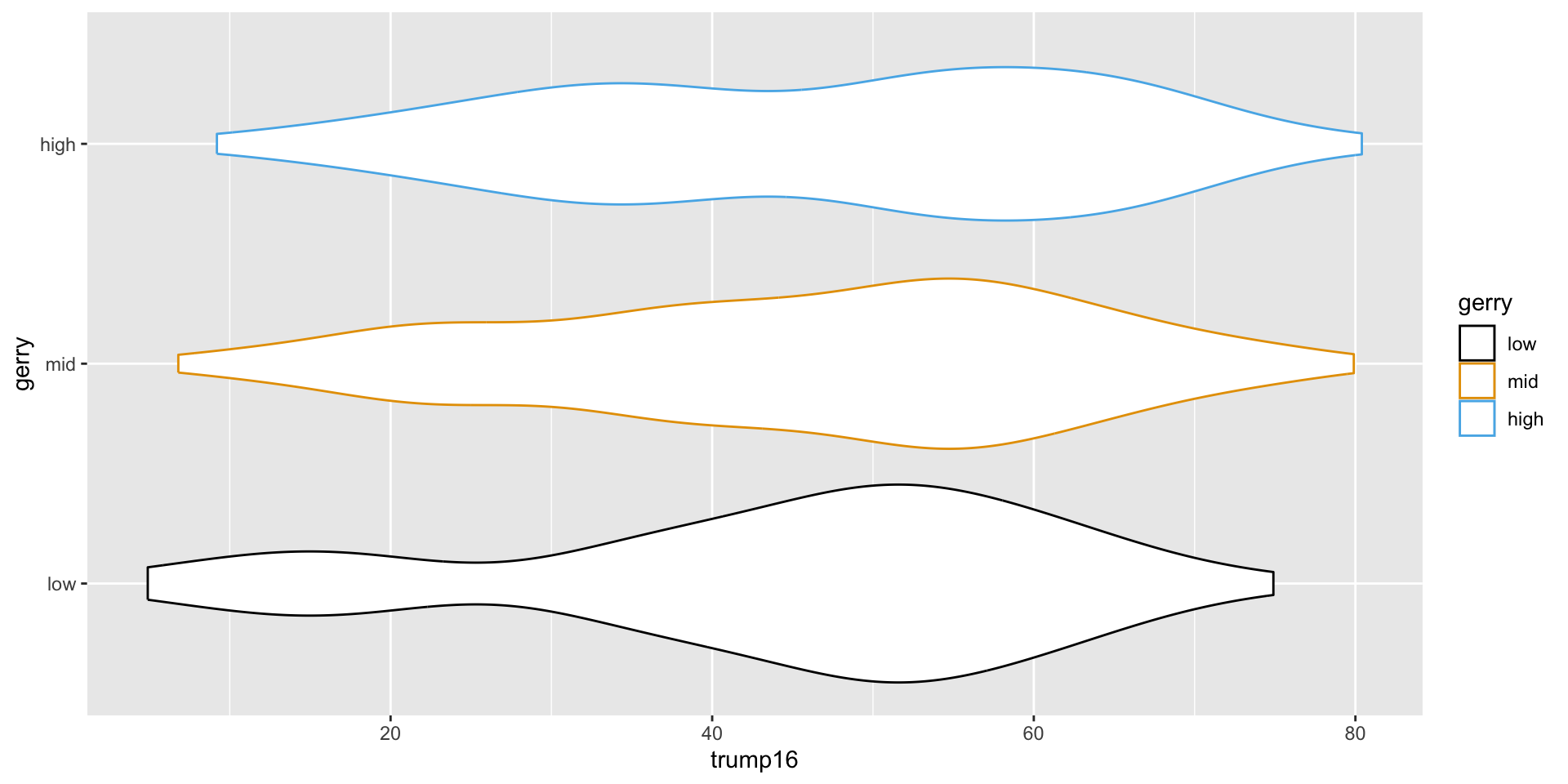
Multiple geoms
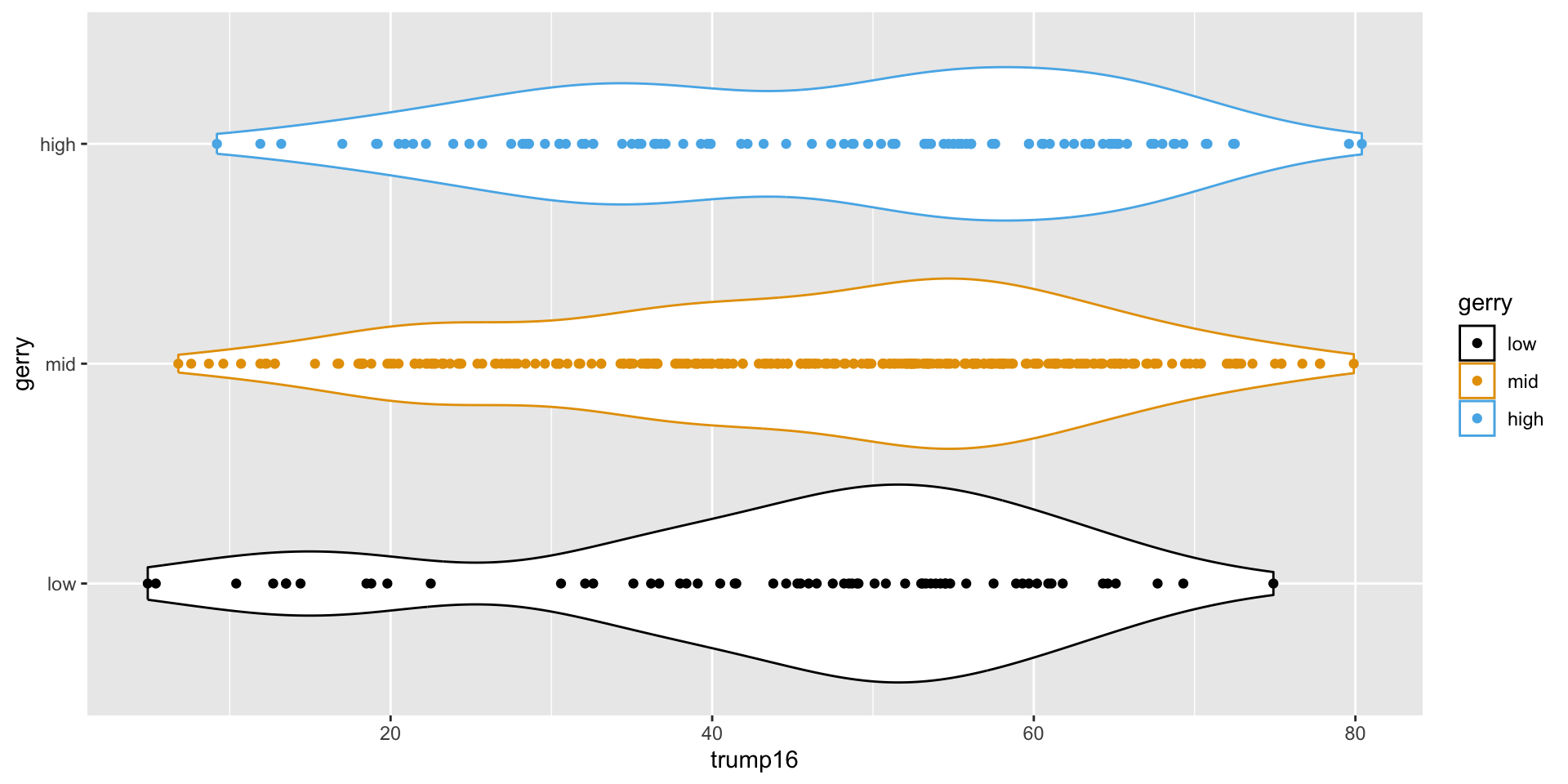
Multiple geoms
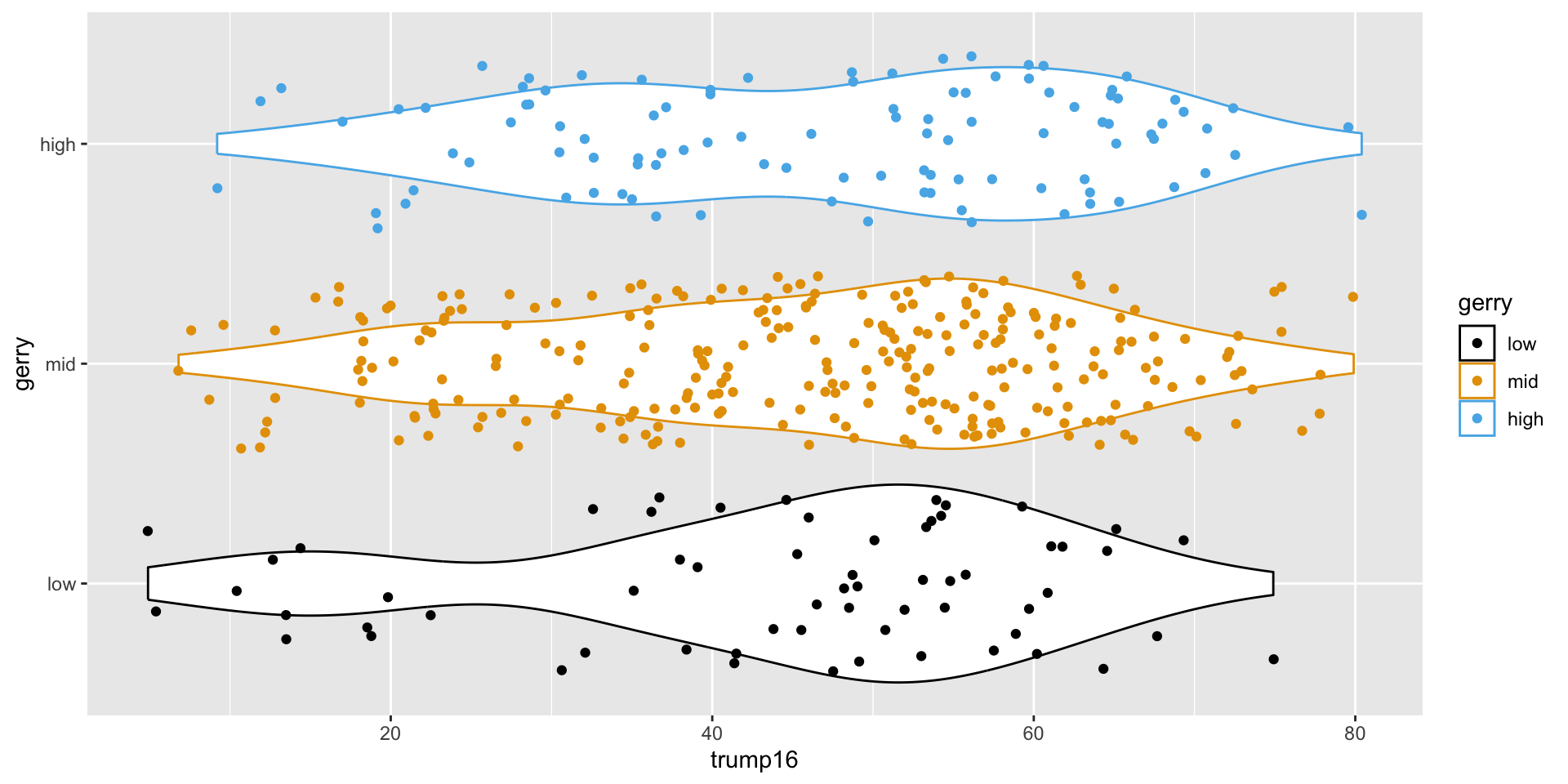
Remove legend
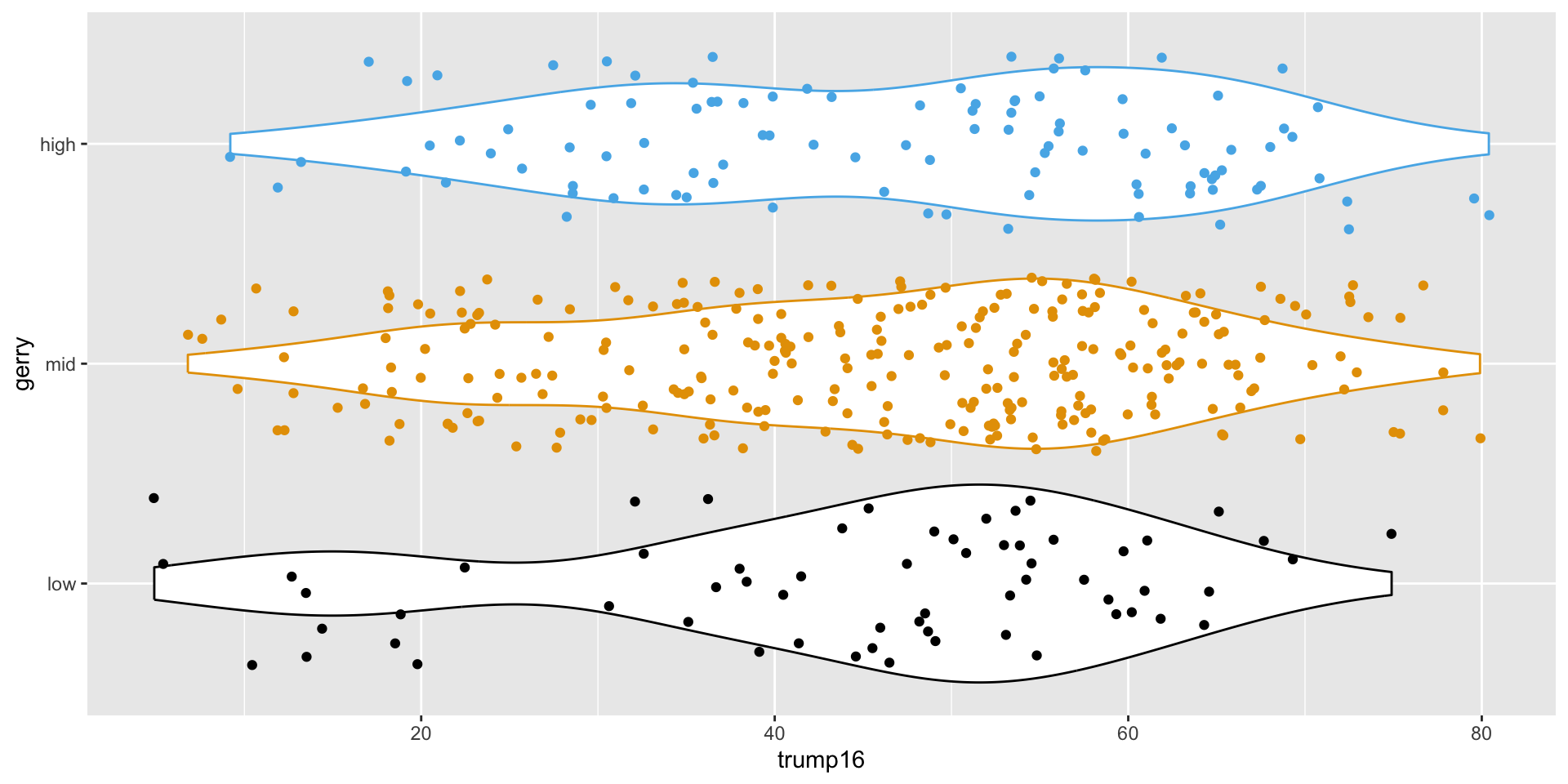
Multivariate analysis
Multivariate analysis
Analyzing the relationship between multiple variables:
In general, one variable is identified as the outcome of interest
The remaining variables are predictors or explanatory variables
-
Plots for exploring multivariate relationships are the same as those for bivariate relationships, but conditional on one or more variables
- Conditioning can be done via faceting or aesthetic mappings (e.g., scatterplot of
yvs.x1, colored byx2, faceted byx3)
- Conditioning can be done via faceting or aesthetic mappings (e.g., scatterplot of
-
Summary statistics for exploring multivariate relationships are the same as those for bivariate relationships, but conditional on one or more variables
- Conditioning can be done via grouping (e.g., correlation between
yandx1, grouped by levels ofx2andx3)
- Conditioning can be done via grouping (e.g., correlation between
Application exercise
ae-04-gerrymander-explore-I
Go to your ae project in RStudio.
If you haven’t yet done so, make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
If you haven’t yet done so, click Pull to get today’s application exercise file: ae-04-gerrymander-explore-I.qmd.
Work through the application exercise in class, and render, commit, and push your edits by the end of class.