Evaluating models

Lecture 20

Dr. Mine Çetinkaya-Rundel

Duke University
STA 199 - Fall 2024

November 12, 2024

Warm-up

While you wait…

Go to your ae project in RStudio.
Make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
Click Pull to get today’s application exercise file: ae-17-forest-classification.qmd.
Wait till the you’re prompted to work on the application exercise during class before editing the file.

Announcements

Project milestone 3 - Improvement and progress due at 5 pm on Friday

Washington forests

Packages

library(tidyverse)
library(tidymodels)
library(forested)

Data

The U.S. Forest Service maintains machine learning models to predict whether a plot of land is “forested.”
This classification is important for research, legislation, land management, etc. purposes.
Plots are typically remeasured every 10 years.
The forested dataset contains the most recent measurement per plot.

Data: `forested`

forested

# A tibble: 7,107 × 19
   forested  year elevation eastness northness roughness tree_no_tree
   <fct>    <dbl>     <dbl>    <dbl>     <dbl>     <dbl> <fct>       
 1 Yes       2005       881       90        43        63 Tree        
 2 Yes       2005       113      -25        96        30 Tree        
 3 No        2005       164      -84        53        13 Tree        
 4 Yes       2005       299       93        34         6 No tree     
 5 Yes       2005       806       47       -88        35 Tree        
 6 Yes       2005       736      -27       -96        53 Tree        
 7 Yes       2005       636      -48        87         3 No tree     
 8 Yes       2005       224      -65       -75         9 Tree        
 9 Yes       2005        52      -62        78        42 Tree        
10 Yes       2005      2240      -67       -74        99 No tree     
# ℹ 7,097 more rows
# ℹ 12 more variables: dew_temp <dbl>, precip_annual <dbl>,
#   temp_annual_mean <dbl>, temp_annual_min <dbl>,
#   temp_annual_max <dbl>, temp_january_min <dbl>, vapor_min <dbl>,
#   vapor_max <dbl>, canopy_cover <dbl>, lon <dbl>, lat <dbl>,
#   land_type <fct>

Data: `forested`

glimpse(forested)

Rows: 7,107
Columns: 19
$ forested         <fct> Yes, Yes, No, Yes, Yes, Yes, Yes, Yes, Yes,…
$ year             <dbl> 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2…
$ elevation        <dbl> 881, 113, 164, 299, 806, 736, 636, 224, 52,…
$ eastness         <dbl> 90, -25, -84, 93, 47, -27, -48, -65, -62, -…
$ northness        <dbl> 43, 96, 53, 34, -88, -96, 87, -75, 78, -74,…
$ roughness        <dbl> 63, 30, 13, 6, 35, 53, 3, 9, 42, 99, 51, 19…
$ tree_no_tree     <fct> Tree, Tree, Tree, No tree, Tree, Tree, No t…
$ dew_temp         <dbl> 0.04, 6.40, 6.06, 4.43, 1.06, 1.35, 1.42, 6…
$ precip_annual    <dbl> 466, 1710, 1297, 2545, 609, 539, 702, 1195,…
$ temp_annual_mean <dbl> 6.42, 10.64, 10.07, 9.86, 7.72, 7.89, 7.61,…
$ temp_annual_min  <dbl> -8.32, 1.40, 0.19, -1.20, -5.98, -6.00, -5.…
$ temp_annual_max  <dbl> 12.91, 15.84, 14.42, 15.78, 13.84, 14.66, 1…
$ temp_january_min <dbl> -0.08, 5.44, 5.72, 3.95, 1.60, 1.12, 0.99, …
$ vapor_min        <dbl> 78, 34, 49, 67, 114, 67, 67, 31, 60, 79, 17…
$ vapor_max        <dbl> 1194, 938, 754, 1164, 1254, 1331, 1275, 944…
$ canopy_cover     <dbl> 50, 79, 47, 42, 59, 36, 14, 27, 82, 12, 74,…
$ lon              <dbl> -118.6865, -123.0825, -122.3468, -121.9144,…
$ lat              <dbl> 48.69537, 47.07991, 48.77132, 45.80776, 48.…
$ land_type        <fct> Tree, Tree, Tree, Tree, Tree, Tree, Non-tre…

Outcome and predictors

Outcome: forested - Factor, Yes or No

levels(forested$forested)

[1] "Yes" "No"

Predictors: 18 remotely-sensed and easily-accessible predictors:
- numeric variables based on weather and topography
- categorical variables based on classifications from other governmental organizations

`?forested`

Should we include a predictor?

To determine whether we should include a predictor in a model, we should start by asking:

Is it ethical to use this variable? (Or even legal?)
Will this variable be available at prediction time?
Does this variable contribute to explainability?

Data splitting and spending

We’ve been cheating!

So far, we’ve been using all the data we have for building models. In predictive contexts, this would be considered cheating.
Evaluating model performance for predicting outcomes that were used when building the models is like evaluating your learning with questions whose answers you’ve already seen.

Spending your data

For predictive models (used primarily in machine learning), we typically split data into training and test sets:

The training set is used to estimate model parameters.
The test set is used to find an independent assessment of model performance.

Warning

Do not use, or even peek at, the test set during training.

How much to spend?

The more data we spend (use in training), the better estimates we’ll get.
Spending too much data in training prevents us from computing a good assessment of predictive performance.
Spending too much data in testing prevents us from computing a good estimate of model parameters.

The initial split

set.seed(20241112)
forested_split <- initial_split(forested)
forested_split

<Training/Testing/Total>
<5330/1777/7107>

Setting a seed

What does set.seed() do?

To create that split of the data, R generates “pseudo-random” numbers: while they are made to behave like random numbers, their generation is deterministic given a “seed”.
This allows us to reproduce results by setting that seed.
Which seed you pick doesn’t matter, as long as you don’t try a bunch of seeds and pick the one that gives you the best performance.

Accessing the data

forested_train <- training(forested_split)
forested_test <- testing(forested_split)

The training set

forested_train

# A tibble: 5,330 × 19
   forested  year elevation eastness northness roughness tree_no_tree
   <fct>    <dbl>     <dbl>    <dbl>     <dbl>     <dbl> <fct>       
 1 Yes       2013       315      -17        98        92 Tree        
 2 No        2018       374       93       -34        23 No tree     
 3 No        2017       377       44       -89         1 Tree        
 4 Yes       2013       541       31       -94       139 Tree        
 5 Yes       2017       680       14       -98        20 Tree        
 6 Yes       2017      1482       76       -64        43 Tree        
 7 No        2020        84       42       -90        12 No tree     
 8 Yes       2011       210       34        93        16 Tree        
 9 No        2020       766       14        98        20 No tree     
10 Yes       2013      1559       98        16        79 Tree        
# ℹ 5,320 more rows
# ℹ 12 more variables: dew_temp <dbl>, precip_annual <dbl>,
#   temp_annual_mean <dbl>, temp_annual_min <dbl>,
#   temp_annual_max <dbl>, temp_january_min <dbl>, vapor_min <dbl>,
#   vapor_max <dbl>, canopy_cover <dbl>, lon <dbl>, lat <dbl>,
#   land_type <fct>

The testing data

🙈

Exploratory data analysis

Initial questions

What’s the distribution of the outcome, forested?
What’s the distribution of numeric variables like precip_annual?
How does the distribution of forested differ across the categorical and numerical variables?

Which dataset should we use for the exploration? The entire data forested, the training data forested_train, or the testing data forested_test?

`forested`

What’s the distribution of the outcome, forested?

`precip_annual`

What’s the distribution of precip_annual?

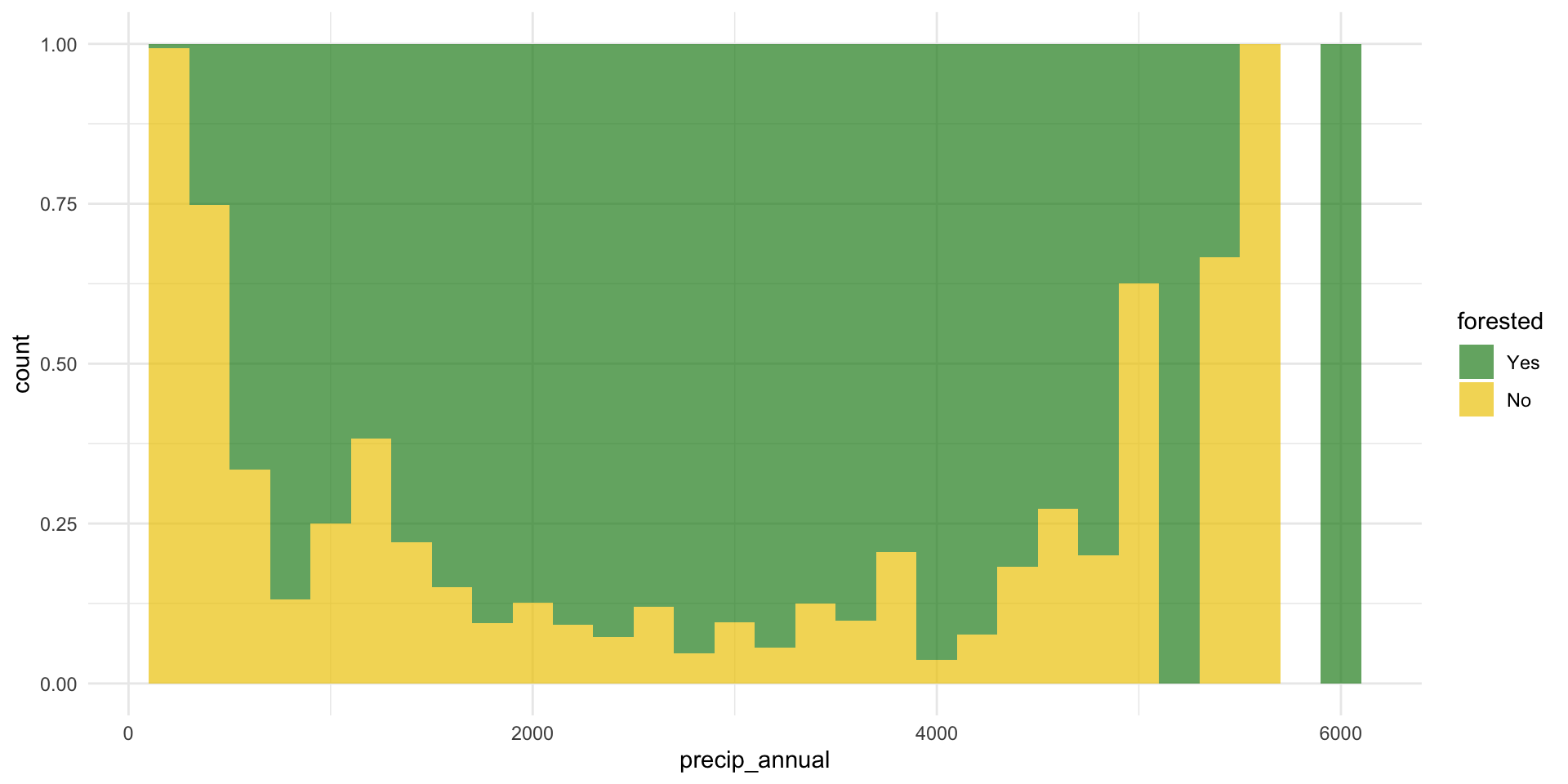
`forested` and `precip_annual`

ggplot(
  forested_train,
  aes(x = precip_annual, fill = forested, group = forested)
  ) +
  geom_histogram(binwidth = 200, position = "identity", alpha = 0.7) +
  scale_fill_manual(values = c("Yes" = "forestgreen", "No" = "gold2")) +
  theme_minimal()

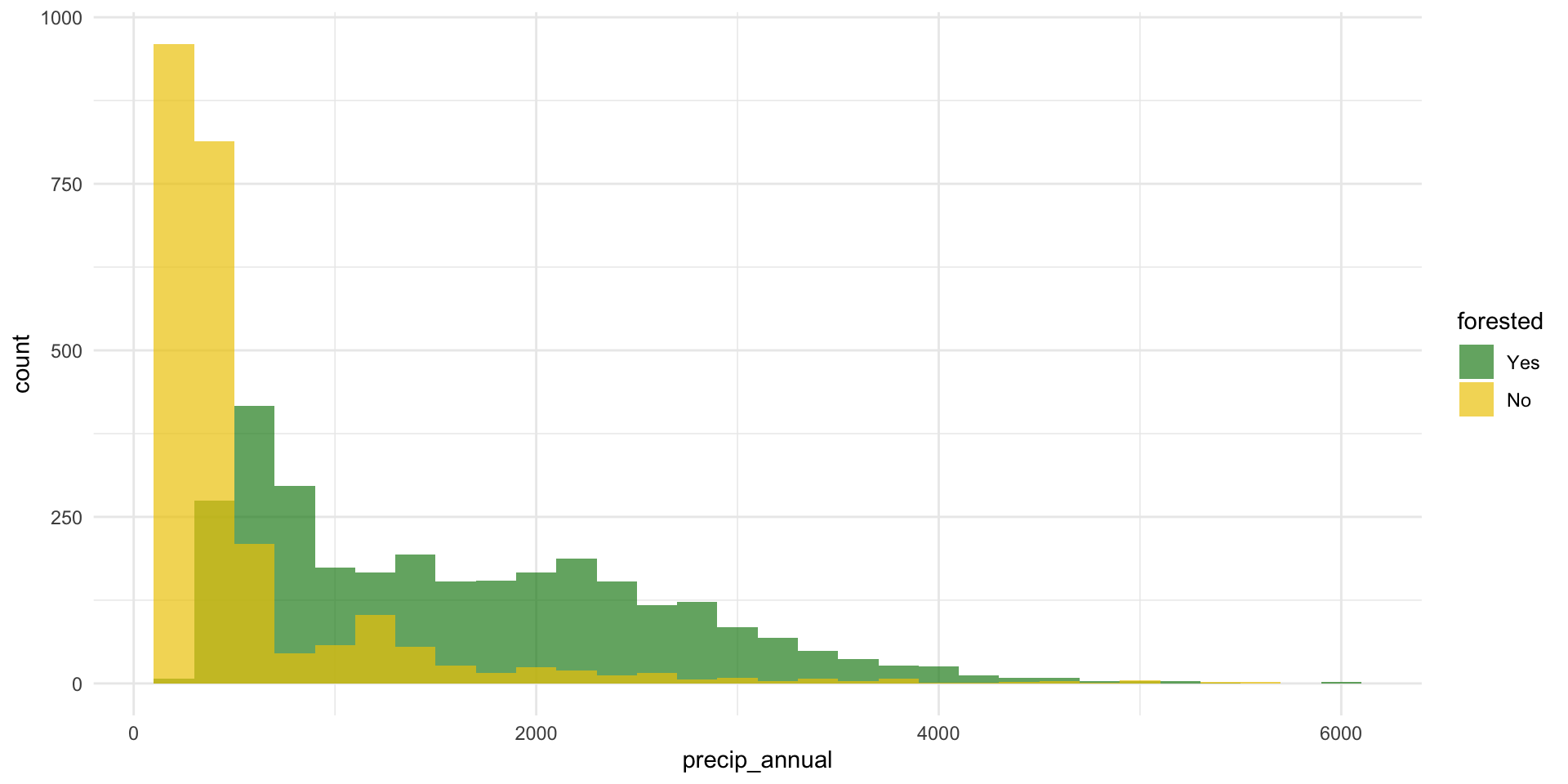
`forested` and `precip_annual`

ggplot(
  forested_train,
  aes(x = precip_annual, fill = forested, group = forested)
  ) +
  geom_histogram(binwidth = 200, position = "fill", alpha = 0.7) +
  scale_fill_manual(values = c("Yes" = "forestgreen", "No" = "gold2")) +
  theme_minimal()

`forested` and `tree_no_tree`

ggplot(forested_train, aes(x = tree_no_tree, fill = forested)) +
  geom_bar(position = "fill") +
  scale_fill_manual(values = c("Yes" = "forestgreen", "No" = "gold2")) +
  theme_minimal()

`forested` and `lat` / `lon`

ggplot(forested_train, aes(x = lon, y = lat, color = forested)) +
  geom_point(alpha = 0.7) +
  scale_color_manual(values = c("Yes" = "forestgreen", "No" = "gold2")) +
  theme_minimal()

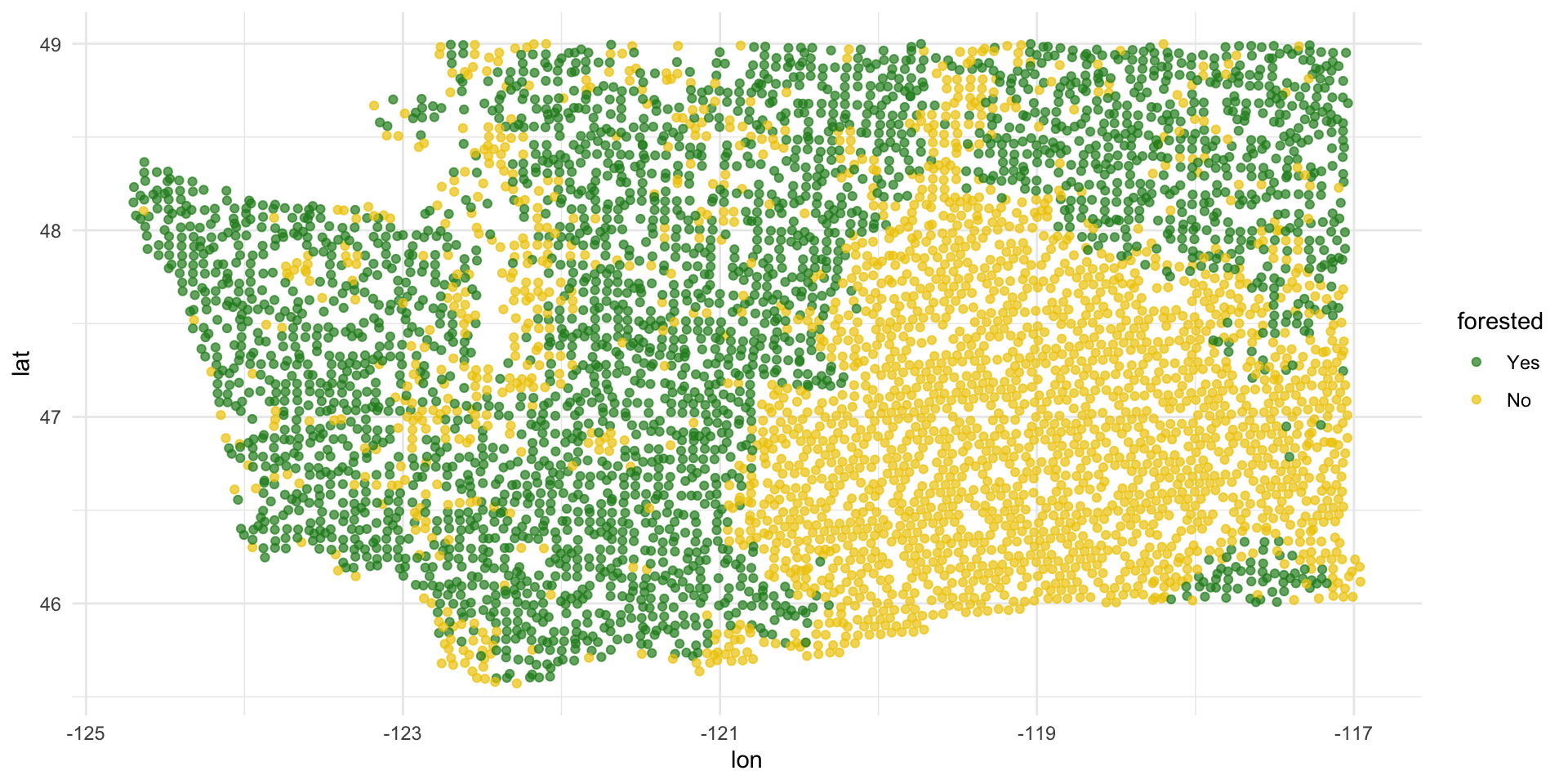
Terminology

False negative and positive

False negative rate is the proportion of actual positives that were classified as negatives.
False positive rate is the proportion of actual negatives that were classified as positives.

Sensitivity

Sensitivity is the proportion of actual positives that were correctly classified as positive.

Also known as true positive rate and recall
Sensitivity = 1 − False negative rate
Useful when false negatives are more “expensive” than false positives

Specificity

Specificity is the proportion of actual negatives that were correctly classified as negative

Also known as true negative rate
Specificity = 1 − False positive rate

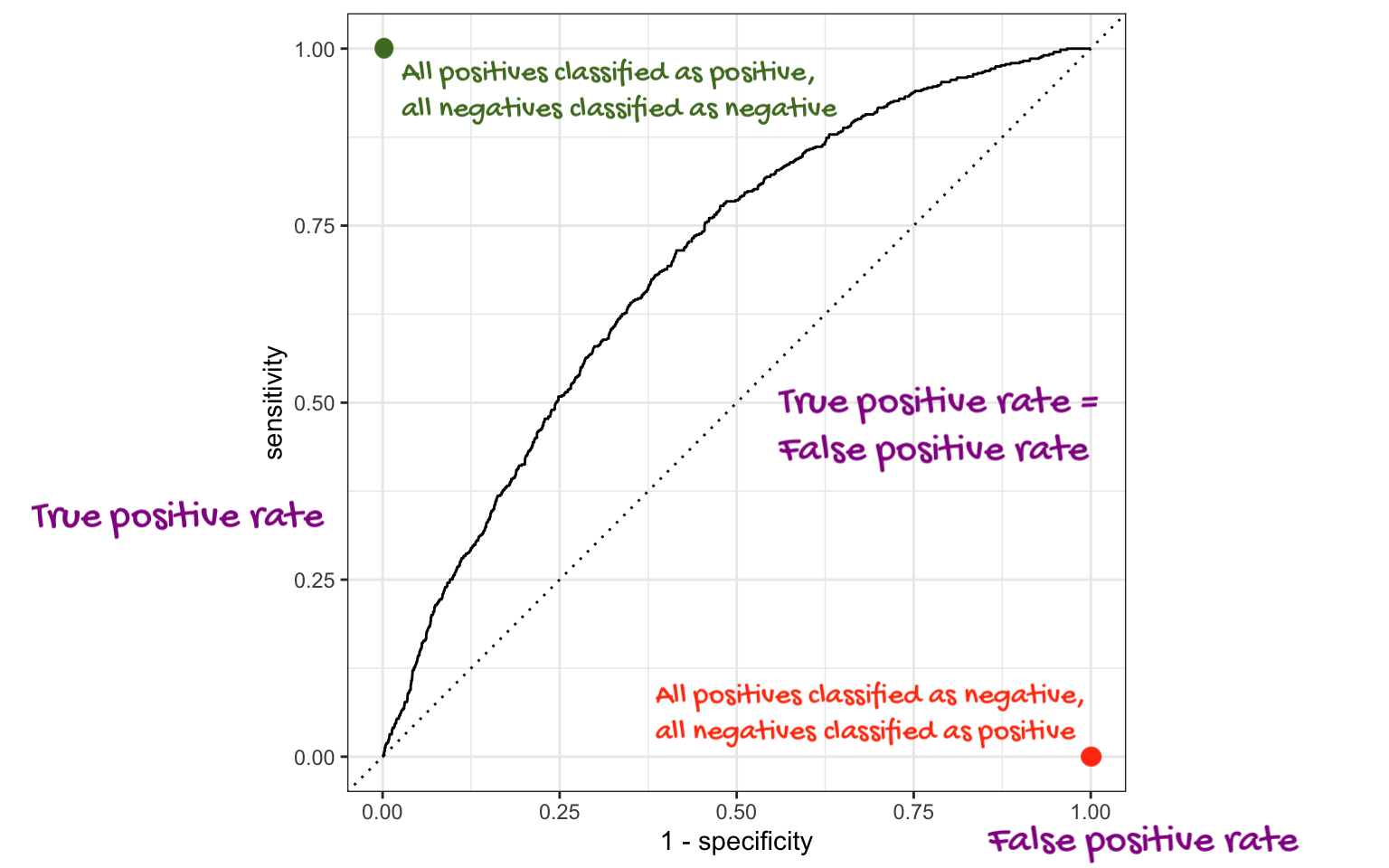
ROC curve

The receiver operating characteristic (ROC) curve allows to assess the model performance across a range of thresholds.

ROC curve

Which corner of the plot indicates the best model performance?

Next steps

Fit models on training data
Make predictions on testing data
Evaluate predictions on testing data:
- Linear models: R-squared, adjusted R-squared, RMSE (root mean squared error), etc.
- Logistic models: False negative and positive rates, AUC (area under the curve), etc.
Make decisions based on model predictive performance, validity across various testing/training splits (aka “cross validation”), explainability

Note

We will only learn about a subset of these in this course, but you can go further into these ideas in STA 210 or STA 221 as well as in various machine learning courses.

ae-17-forest-classification

Go to your ae project in RStudio.
If you haven’t yet done so, make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.
If you haven’t yet done so, click Pull to get today’s application exercise file: ae-17-forest-classification.qmd. You might be prompted to install forested, say yes.
Work through the application exercise in class, and render, commit, and push your edits.

Evaluating models

Warm-up

While you wait…

Announcements

Washington forests

Packages

Data

Data: forested

Data: forested

Outcome and predictors

?forested

Should we include a predictor?

Data splitting and spending

We’ve been cheating!

Spending your data

How much to spend?

The initial split

Setting a seed

Accessing the data

The training set

The testing data

Exploratory data analysis

Initial questions

forested

precip_annual

forested and precip_annual

forested and precip_annual

forested and tree_no_tree

forested and lat / lon

Terminology

False negative and positive

Sensitivity

Specificity

ROC curve

ROC curve

Next steps

Next steps

ae-17-forest-classification

Data: `forested`

Data: `forested`

`?forested`

`forested`

`precip_annual`

`forested` and `precip_annual`

`forested` and `precip_annual`

`forested` and `tree_no_tree`

`forested` and `lat` / `lon`