Inference overview

Lecture 23

Author
Affiliation

Dr. Mine Çetinkaya-Rundel

Duke University
STA 199 - Fall 2024

Published

November 21, 2024

Warm-up

While you wait…

  • Go to your ae project in RStudio.

  • Make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.

  • Click Pull to get today’s application exercise file: ae-19-equality-randomization.qmd.

  • Wait till the you’re prompted to work on the application exercise during class before editing the file.

From last time: Randomization

Packages

# load packages
library(tidyverse)   # for data wrangling and visualization
library(tidymodels)  # for modeling
library(openintro)   # for Duke Forest dataset
library(scales)      # for pretty axis labels
library(glue)        # for constructing character strings
library(knitr)       # for neatly formatted tables

Data: Houses in Duke Forest

  • Data on houses that were sold in the Duke Forest neighborhood of Durham, NC around November 2020
  • Scraped from Zillow
  • Source: openintro::duke_forest

Home in Duke Forest

Setting hypotheses

  • Null hypothesis, \(H_0\): “There is nothing going on.” The slope of the model for predicting the prices of houses in Duke Forest from their areas is 0, \(\beta_1 = 0\).

  • Alternative hypothesis, \(H_A\): “There is something going on”. The slope of the model for predicting the prices of houses in Duke Forest from their areas is different than 0, \(\beta_1 \ne 0\).

Calculate observed slope

… which we have already done:

observed_fit <- duke_forest |>
  specify(price ~ area) |>
  fit()

observed_fit
# A tibble: 2 × 2
  term      estimate
  <chr>        <dbl>
1 intercept  116652.
2 area          159.

Simulate null distribution

set.seed(20241118)
null_dist <- duke_forest |>
  specify(price ~ area) |>
  hypothesize(null = "independence") |>
  generate(reps = 100, type = "permute") |>
  fit()

View null distribution

null_dist
# A tibble: 200 × 3
# Groups:   replicate [100]
   replicate term        estimate
       <int> <chr>          <dbl>
 1         1 intercept 547294.   
 2         1 area           4.54 
 3         2 intercept 568599.   
 4         2 area          -3.13 
 5         3 intercept 561547.   
 6         3 area          -0.593
 7         4 intercept 526286.   
 8         4 area          12.1  
 9         5 intercept 651476.   
10         5 area         -33.0  
# ℹ 190 more rows

Visualize null distribution

null_dist |>
  filter(term == "area") |>
  ggplot(aes(x = estimate)) +
  geom_histogram(binwidth = 15)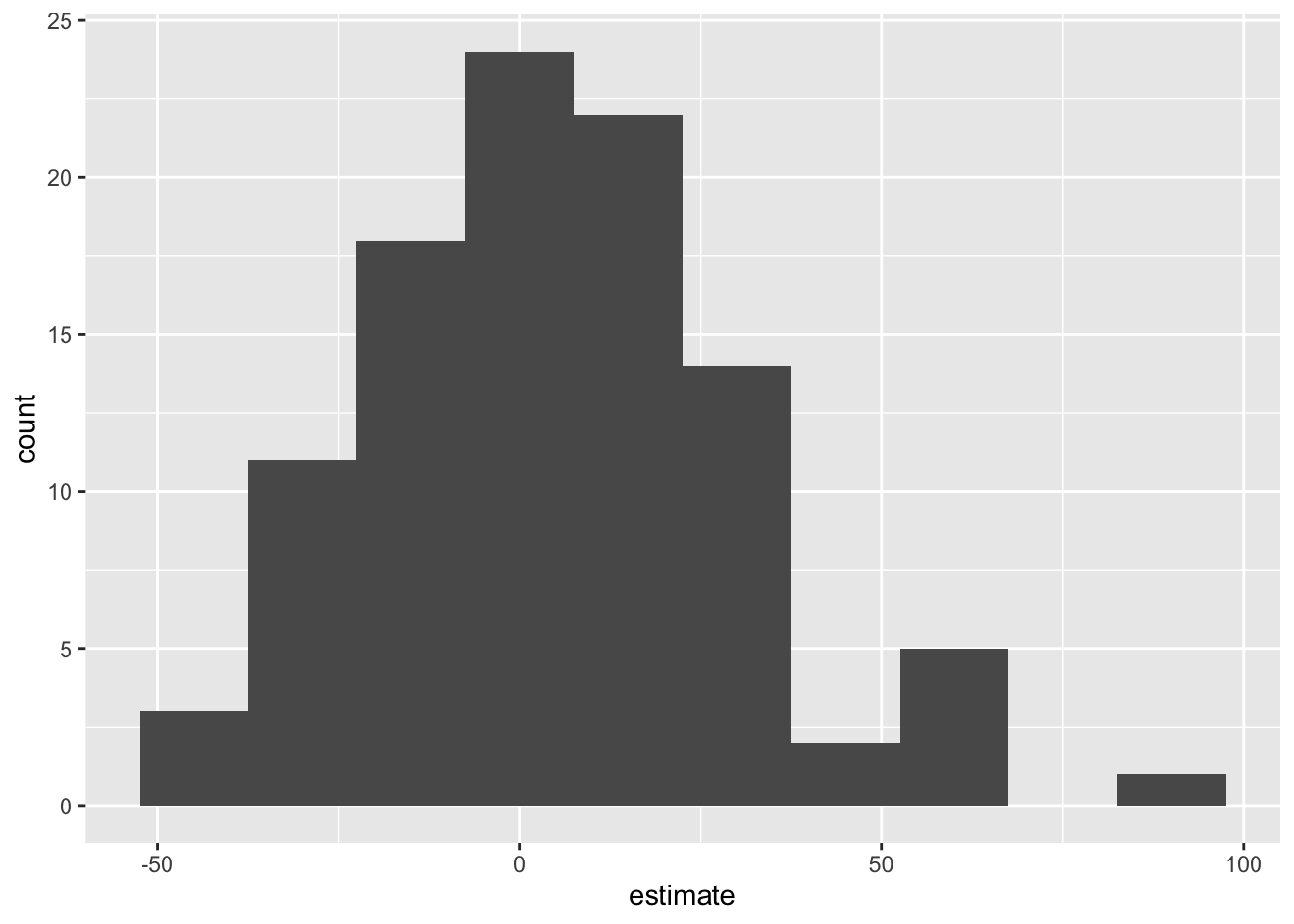

Visualize null distribution (alternative)

visualize(null_dist) +
  shade_p_value(obs_stat = observed_fit, direction = "two-sided")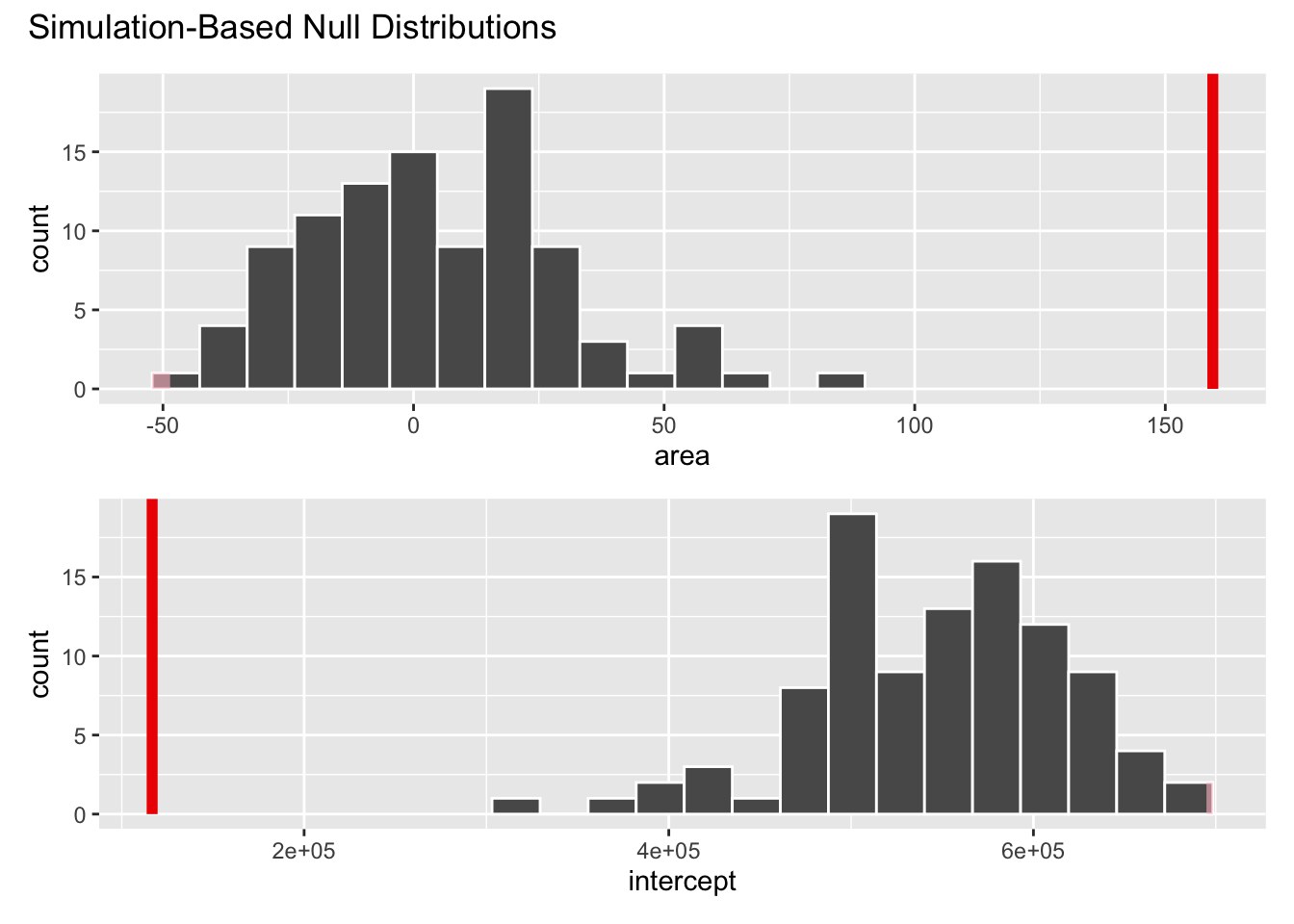

Get p-value

null_dist |>
  get_p_value(obs_stat = observed_fit, direction = "two-sided")
Warning: Please be cautious in reporting a p-value of 0. This result is an
approximation based on the number of `reps` chosen in the
`generate()` step.
ℹ See `get_p_value()` (`?infer::get_p_value()`) for more information.
Please be cautious in reporting a p-value of 0. This result is an
approximation based on the number of `reps` chosen in the
`generate()` step.
ℹ See `get_p_value()` (`?infer::get_p_value()`) for more information.
# A tibble: 2 × 2
  term      p_value
  <chr>       <dbl>
1 area            0
2 intercept       0

Make a decision

Based on the p-value calculated, what is the conclusion of the hypothesis test?

Inference for a mean

Estimating the average price of houses in Duke Forest

Estimate the average price of houses in Duke Forest with a 95% confidence interval.

Computing the CI for the mean I

Calculate the observed mean:

observed_mean <- duke_forest |>
  specify(response = price) |>
  calculate(stat = "mean")

observed_mean
Response: price (numeric)
# A tibble: 1 × 1
     stat
    <dbl>
1 559899.

Computing the CI for the mean II

Take 100 bootstrap samples and calculate the mean of each one:

set.seed(1121)

boot_means <- duke_forest |>
  specify(response = price) |>
  generate(reps = 100, type = "bootstrap") |>
  calculate(stat = "mean")

boot_means
Response: price (numeric)
# A tibble: 100 × 2
   replicate    stat
       <int>   <dbl>
 1         1 591471.
 2         2 545975.
 3         3 588256.
 4         4 569751.
 5         5 566394.
 6         6 583654.
 7         7 533031.
 8         8 575321.
 9         9 559893.
10        10 588826.
# ℹ 90 more rows

Computing the CI for the mean III

Compute the 95% CI as the middle 95% of the bootstrap distribution:

get_confidence_interval(
  boot_means, 
  point_estimate = observed_mean, 
  level = 0.95,
  type = "percentile"
)
# A tibble: 1 × 2
  lower_ci upper_ci
     <dbl>    <dbl>
1  521923.  605514.

Making a decision about the average price of houses in Duke Forest

An article in the Durham Herald Sun states that the average price of a house in Duke Forest is $600,000. Do these data provide convincing evidence to refute this claim?

Setting the hypotheses

Define \(\mu\) as the true average price of all houses in Duke Forest:

  • \(H_0: \mu = 600000\) - The true average price of all houses in Duke Forest is $600,000 (as claimed by the Durham Herald Sun, i.e., there’s nothing going on)

  • \(H_A: \mu \ne 600000\) - The true average price of all houses in Duke Forest is different than $600,000 (refuting the claim by the Durham Herald Sun, i.e., there is something going on)

Calculate the observed

Well, we already did this!

observed_mean
Response: price (numeric)
# A tibble: 1 × 1
     stat
    <dbl>
1 559899.

Simulate the null distribution

set.seed(1121)

null_means <- duke_forest |>
  specify(response = price) |>
  hypothesize(null = "point", mu = 600000) |>
  generate(reps = 100, type = "bootstrap") |>
  calculate(stat = "mean")

null_means
Response: price (numeric)
Null Hypothesis: point
# A tibble: 100 × 2
   replicate    stat
       <int>   <dbl>
 1         1 631572.
 2         2 586077.
 3         3 628357.
 4         4 609853.
 5         5 606495.
 6         6 623755.
 7         7 573132.
 8         8 615423.
 9         9 599994.
10        10 628927.
# ℹ 90 more rows

Visualize the null distribution

visualize(null_means)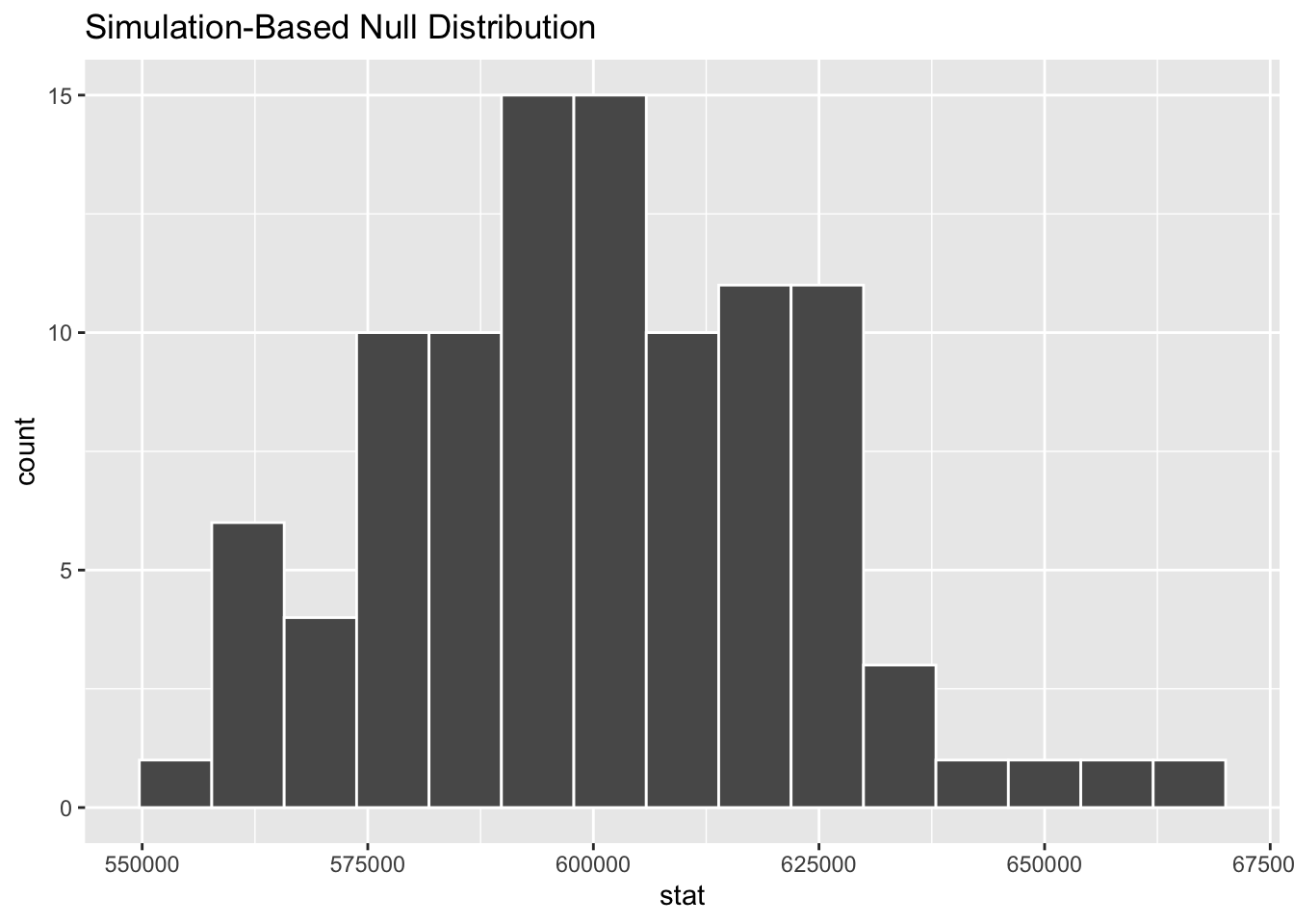

Calculate the p-value

  • Probability of observed or lower outcome, given the given the null hypothesis is true: \(P(\bar{x} < 559899 ~ | ~ \mu = 600000)\)

. . .

  • Probability of observed or more extreme outcome, given the null hypothesis is true:

\[ 2 \times P(\bar{x} < 559899 ~ | ~ \mu = 600000) \]

. . .

null_means |>
  get_p_value(
    obs_stat = observed_mean, 
    direction = "two-sided"
  )
# A tibble: 1 × 1
  p_value
    <dbl>
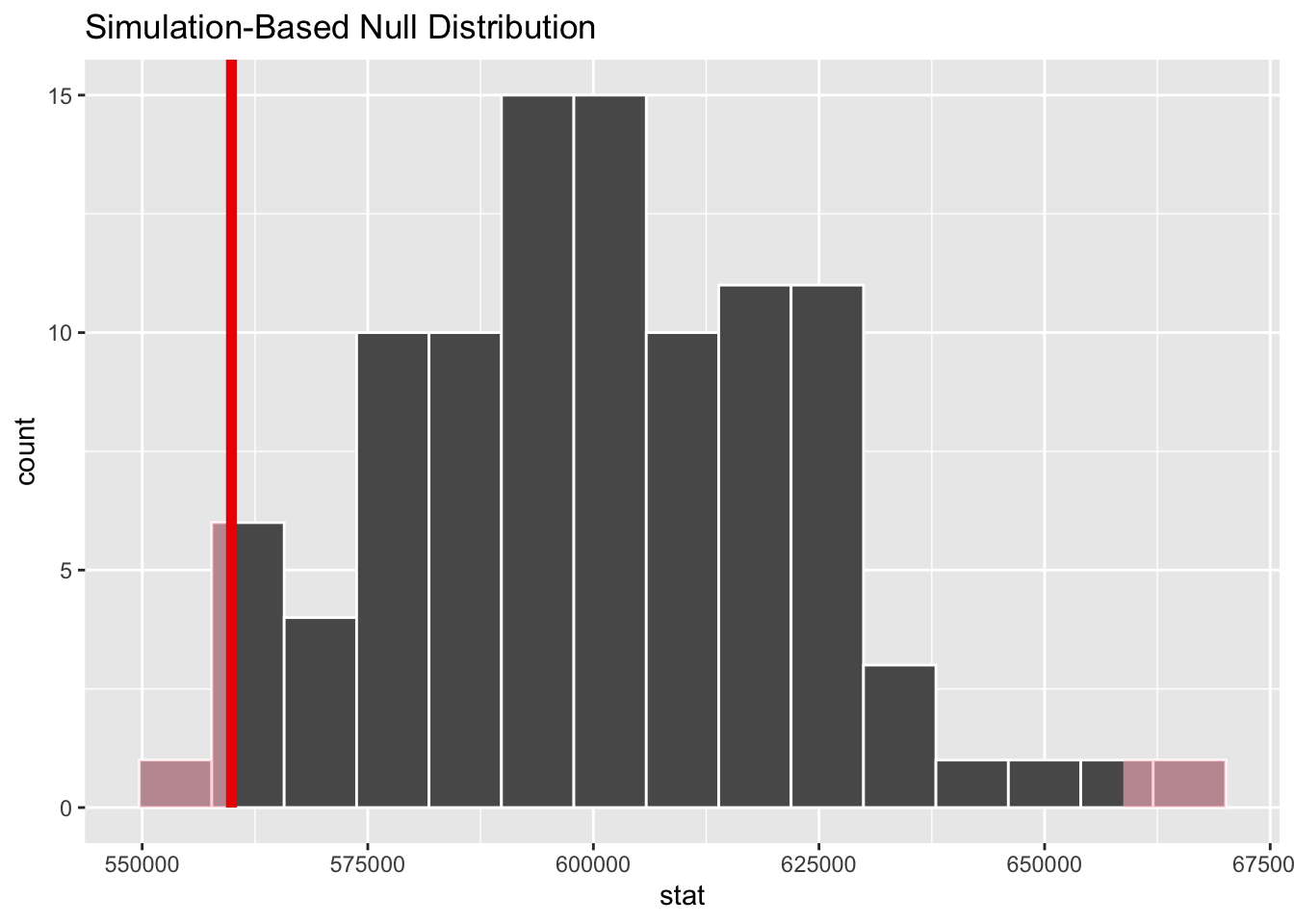
1    0.02

Visualize the p-value

visualize(null_means) +
  shade_p_value(
    obs_stat = observed_mean, 
    direction = "two-sided"
  )

Application exercise

ae-19-equality-randomization

  • Go to your ae project in RStudio.

  • If you haven’t yet done so, make sure all of your changes up to this point are committed and pushed, i.e., there’s nothing left in your Git pane.

  • If you haven’t yet done so, click Pull to get today’s application exercise file: ae-19-equality-randomization.qmd.

  • Work through the application exercise in class, and render, commit, and push your edits.

Recap of AE

  • A hypothesis test is a statistical technique used to evaluate competing claims (null and alternative hypotheses) using data.
  • We simulate a null distribution using our original data.
  • We use our sample statistic and direction of the alternative hypothesis to calculate the p-value.
  • We use the p-value to determine conclusions about the alternative hypotheses.